Statistical Physics of Coupled Oscillator Networks (GitHub)

This video shows the collective behavior of 65,536 noisy coupled nonlinear two-cycle oscillators occupying each node of a 2D grid. The oscillators lying within each black cluster are synchronized with each other but are out-of-sync with the oscillators in surrounding white clusters. We have shown that this collective behavior of a coupled oscillator network is identical to the collective behavior of a two-state magnetic spin system, such as iron, near a critical transition from permanent to non-permanent magnetism and of certain liquid-vapor transitions. These theoretical results are based on large-scale Monte Carlo simulations optimized in C++ and distributed over 192 threads of a High Performance Computing Cluster. Over 100GB of simulated data were analyzed and visualized in Python (numpy, scipy, matplotlib). Machine learning techniques were used to perform statistical inference on an Undirected Graphical Model (or Markov Random Field). Following the publication of this theoretical work, we discovered observational evidence of critical behavior in the collective behavior of pistachio trees, which exhibit noisy cycles in annual yield. This research was supported by an NSF INSPIRE award, jointly funded by the Directorates for Mathematical and Physical Sciences (MPS) and Biological Sciences (BIO). Special thanks to Jim Sethna, Steve Strogatz, and Dan Stein for their feedback and support. We also thank the Santa Fe Institute for hosting 3 Working Groups in support of our research. An additional 4-year, $1M non-traditional NSF award supports on-going research.

Noble, AE, Rosenstock, TS, Brown, PH, Machta, J, and Hastings, A. (2018) Spatial Patterns of Tree Yield Explained by Endogenous Forces Through a Correspondence Between the Ising Model and Ecology. PNAS. 115: 8. (open source) [journal]

Noble, AE, Machta, J, and Hastings, A. (2015) Emergent Long-range Synchronization of Oscillating Ecological Populations Without External Forcing Described by Ising Universality. Nature Communications. 6: 6664. (open source) [journal]

Network Anomaly Detection (GitHub)

Detecting anomalies in big spatiotemporal data sets is vitally important to many areas of industry, including the tech, health, financial, and power sectors. Rapid detection and mitigation capabilities are needed to prevent localized distruptions or outbreaks from propagating across large networks. A Principal Component Analysis (PCA) is one approach to de-noising and dimensional reduction of spatiotemporal data in order to establish a baseline against which anomalies can be detected on fast timescales. The leading principal components are also key baseline statistics that predictive spatiotemporal process models should be able to reproduce. I collaborated with Bryan Grenfell and Ottar Bjornstad on an investigation of how the PCA approach might improve upon exisiting epidemiological models of measles outbreaks in the UK following World War II. The video above is a visualization of a portion of that data. The diameter of each disk is proportional to the number of measles cases reported biweekly for each of the sixty largest UK cities. A PCA can also detect anomalies in 1GB of operations data from the San Fransisco bike share program. All of these analyses were performed in Python (cartopy, matplotlib, numpy, pandas).

Mutivartiate Stochastic Processes for Population Biology and Game Theory

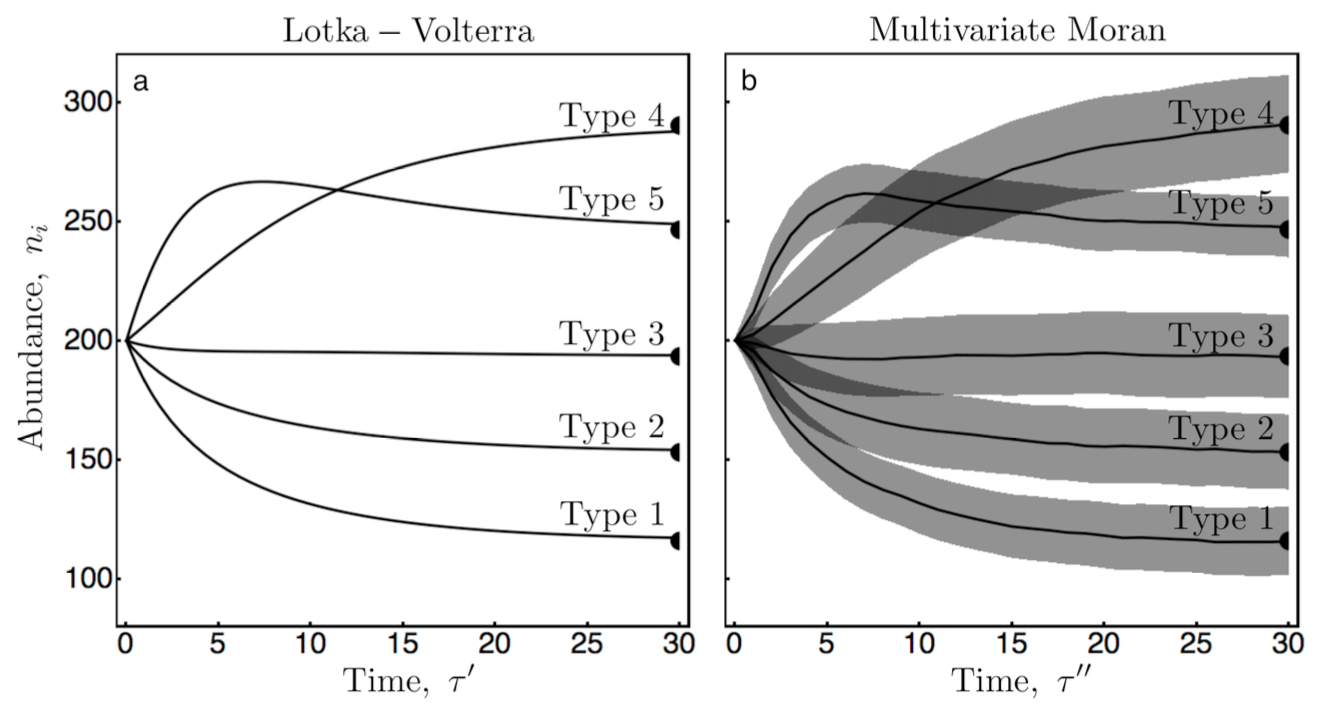
Nonlinear stochastic processes generally require a numerical solution, and the numerical simulation of a multivariate stochastic process can be computationally expensive. The figure here illustrates a scenario in which the dynamics of a nonlinear multivariate stochastic process (panel b) can be predicted based on the much simpler analysis of a purely deterministic system of ordinary differential equations (panel a). Numerical simulations were performed in Python (numpy, scipy); results were plotted in Mathematica. Matching conditions for the stochastic process and deterministic system were obtained from the construction and analysis of a nonlinear multivariate Markov Chain.

Noble, AE, Hastings, A, and Fagan, WF. (2011) Multivariate Moran Process with Lotka-Volterra Phenomenology. Physical Review Letters 107: 228101. [journal][arXiv]

Constraining Particle Physics Models of the Higgs Boson

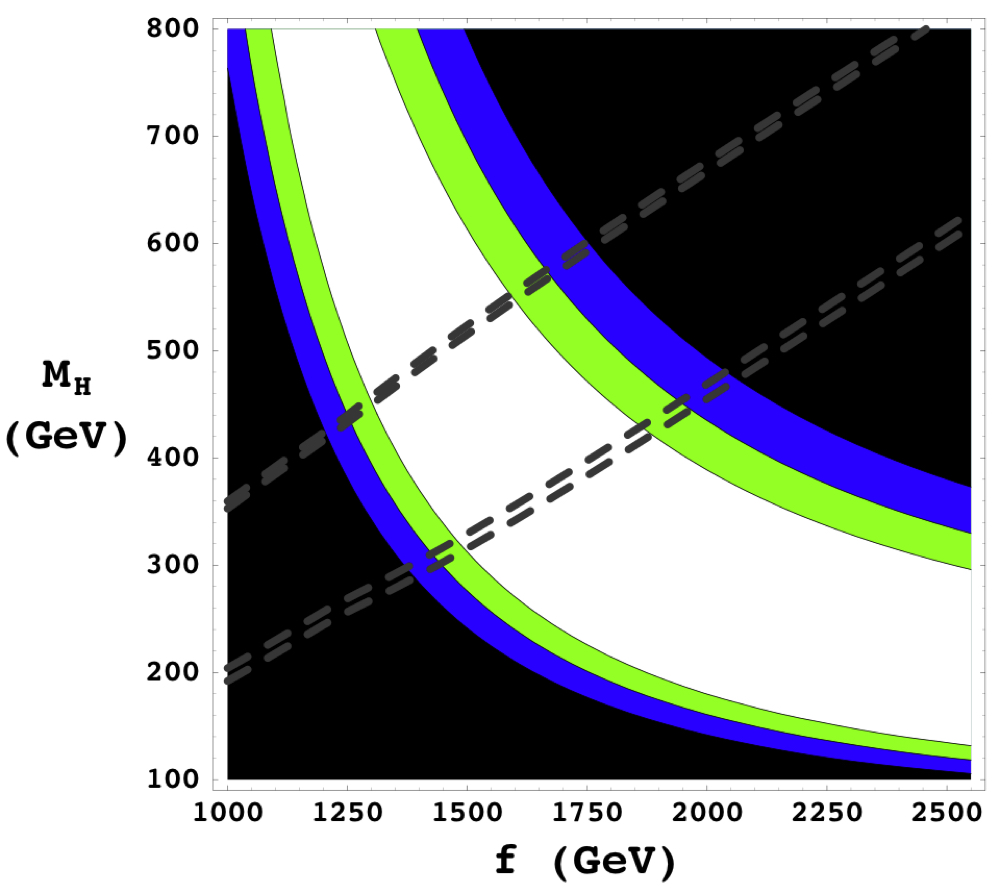
My Ph. D. research in theoretical particle physics focused on confronting models with data. Measurements from terrestrial colliders and satellite observatories can be combined to place tight constraints on hypothetical models for new particles and forces. The figure shown here is based on Feynman diagram calculations and least-squares regressions performed in Mathematica. White indicates the region of the two-dimensional model parameter space that is consistent with collider data at the 95% C.L. or better. Green and blue regions are consistent at the 99% and 99.9% C.L., respectively. The narrow bands of parameter space lying between each of two sets of dashed lines are consistent, at the 95% C.L., with satellite-based constraints on the density of dark matter in the universe. In contrast to many other models for new physics in 2008, joint constraints from collider and satellite data did not rule out the existence of a heavy Higgs

Hubisz, J, Meade, P, AE Noble, and Perelstein, M. (2005) Electroweak Precision Constraints on the Littlest Higgs Model with T Parity. Journal of High Energy Physics 74: 035002. [journal][inspire]